National IQ is the Best Predictor of Economic Growth

Bayesian model averaging and IV regressions of Economic Growth

Emil Kirkegaard and I have a new paper out - National Intelligence and Economic Growth: a Bayesian Update. You can read it here. It’s long so maybe flick through the abstract, figures and the spicy conclusion. You can read Emil’s blog post about the paper here. In a week or two, I will also be releasing an introduction to the IQ and Economic Growth literature suitable for people with no background knowledge. 

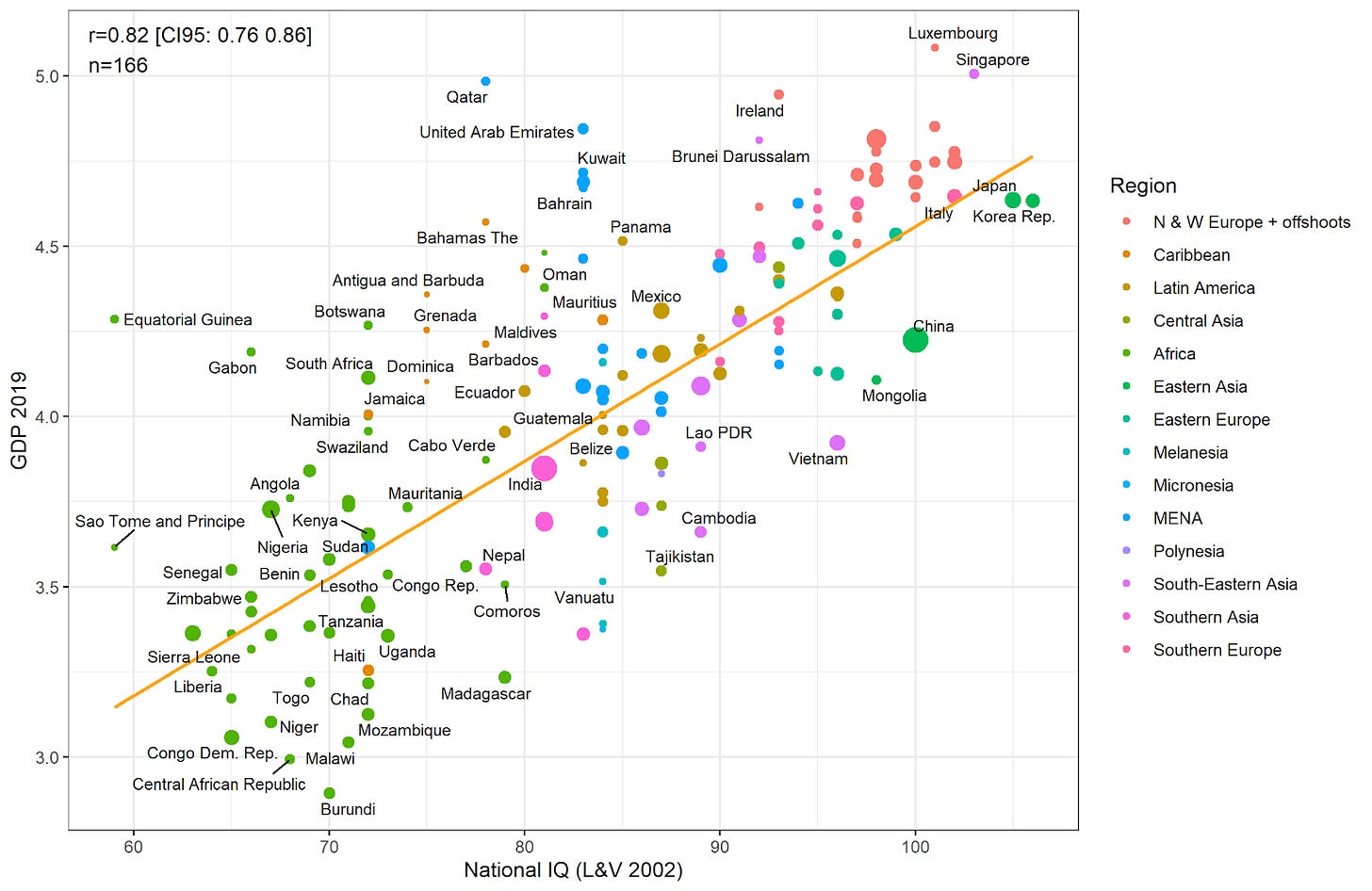
If you have heard of national IQ before then you have probably seen something like the graph below. National Intelligence has an extremely strong association with GDP per capita - roughly 70% of the variation in the wealth of nations can be explained by IQ alone. In fact, it has a very strong relationship with pretty much every national indicator for success. 

This powerful, simple association poses two key questions:

1. Is the relationship causal? Is intelligence causing GDP?

and

2. If so, is this the best explanation of the wealth of nations?

Our new paper answers both questions with an emphatic yes. We find national IQ to be the most robust predictor of economic growth with the largest effect size, compared to +70 variables in the growth literature. And the cherry on top is that it is causally identified. In fact, we originally planned to title the paper National Intelligence is the Best Predictor of Economic Growth.

Let’s start with question 2. Although our correlation is extremely strong, many plausible rival explanations also work well - natural resources, institutions, culture etc.. Let’s imagine we have 50 plausible explanatory variables to explain economic growth with. The maths of this implies that there are 2^50, or over one ‘quadrillion’, possible models you can test. Which should we test? With this massive ‘model uncertainty’, the early economic growth literature of the 90s was filled with papers with conflicting results, since economists could alter the methodology, time period and variables to find just those models which happened to support their theory by chance. This p-hacking was bad - a 1993 review of the literature on democracy and economic growth found that nearly half of the published studies suggested democracy improved economic growth and nearly another half said the opposite!

How can we understand economic growth if researchers only show a biased sample of the possible models? It’s simple - take an unbiased sample of all the possible models and report that. From this idea, ‘Bayesian model averaging’ was born. Sala-i-Martin famously published the paper “I Just Ran Two Million Regressions” in which he took all the major proposed predictors of growth and ran all the possible regression models with them. He then took an average of the results of these models, weighted by how well they fitted the data. 

With this tool of Bayesian model averaging, in 2006 Garett Jones and Joel Schneider tested the effectiveness of national IQ in hundreds of thousands of models with competing variables. They reported two key statistics. First was the effect size of national IQ on economic growth, which implied that each national IQ point increased GDP per capita by 6.1%. They also reported its ‘posterior inclusion probability’ (PIP). Crudely this is understood as the probability that national IQ should be put in our model of economic growth. But technically, it is the proportion of the tested models national IQ was in, weighted by how well those models fit the data. The PIP for IQ was 96%, sounds good.

It was an excellent paper, but it hasn’t answered our key question - how well does national IQ perform relative to other predictors? The authors didn’t report their full results. 15 years later we still don’t know exactly how impressive or important national IQ is to economic growth.

But it gets worse. Later papers by economists would claim Bayesian model averaging, just as the literature that came before it, is too sensitive to researcher degrees of freedom. For example, Ciccone and Jarocinski in their paper Determinants of Economic Growth: Will Data Tell? found that the ‘Investment Price’ variable, could move from having a posterior inclusion probability of 98% to 2% depending upon which GDP data was used. There are many similar sorts of results. In a paper co-authored by John Ioannidis, Determinants of economic growth: Different time different answer? it was found that Bayesian model averaging could not consistently identify predictors that were robust across multiple time periods studied. Other papers tried strengthening the method, with different ‘bayesian priors’ or by fixing some variables to be in all the models tried. Yet these papers failed to distinguish some variables as being more important than others. 

Overall the current conclusion in the literature is that of ‘robust ambiguity’. The economists tell us that the data and methods just aren’t good enough to distinguish the best predictors of economic growth. But none of this literature tried testing national IQ. Perhaps the data doesn’t tell, or perhaps the economists have just been using the wrong data. 

So we tried using Bayesian model averaging of economic growth with national IQ as an explanatory variable and including GDP per capita as a control variable in every model (as is done in the prior literature). But this time we reported the results for all the variables and they were standardised so we could compare their effect sizes. What’s more, we tried all the robustness tests we could imagine - different time periods, different bayesian priors, different datasets (created by prestigious economists - we didn’t p-hack our own datasets), different national accounting (GDP) data, bootstrap resampling, jackknifing and many more. We also used different measures of national intelligence, Lynn’s, Becker’s, Rindermann’s, the World Bank’s and the OECD’s. You name a robustness test, we tried it. So what did we find? could the data tell or was national IQ only successful in some model averages? 

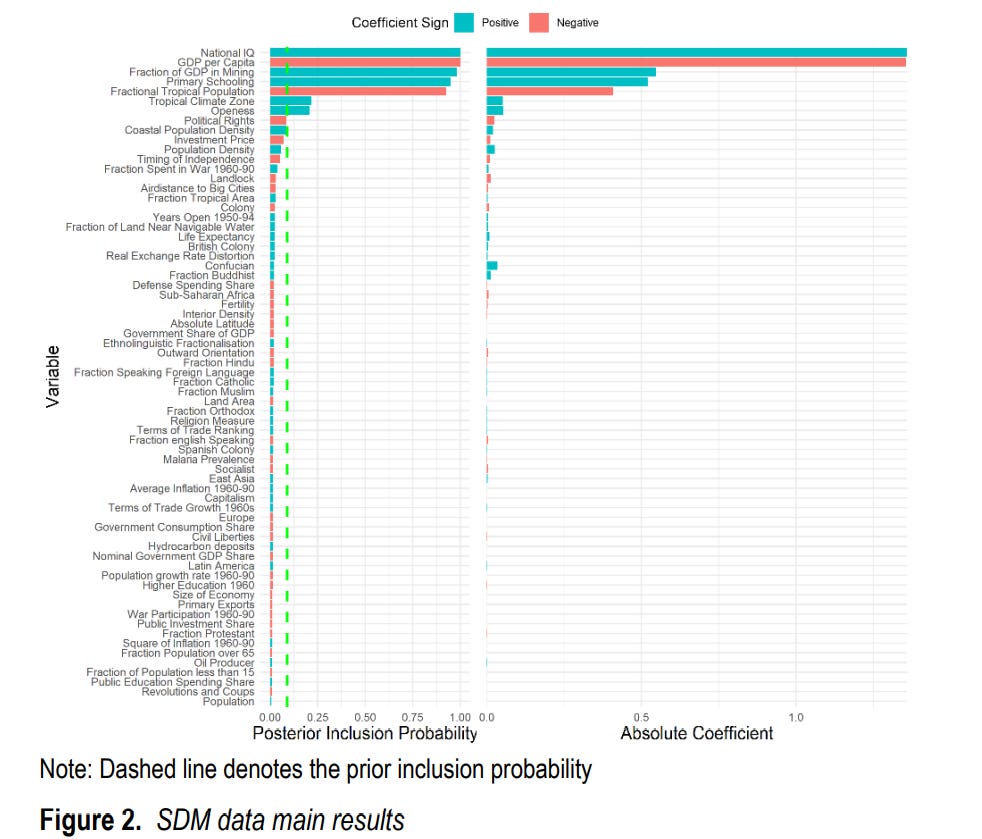
Across every single test, national IQ performed the best with on average the largest standardised coefficient and the largest posterior inclusion probability (PIP). Well except for GDP per capita in the starting year, which we forced into every model anyway. In every Bayesian model averaging, national IQ’s PIP was higher than its prior inclusion probability. Our results pretty much always looked like this:

National IQ dominates the other tested variables and it kept doing so. Whilst in this graph some of the other explanatory variables do perform well, they drop off in our other robustness tests. National IQ reigns king. When we put our results into a Solow-style model of economic growth (details are in the appendix of the paper), each national IQ point was associated with a 7.8% increase in GDP per capita. 

We did lots of other cool stuff with the model averaging too, such as testing smart fraction theory (it doesn’t perform well) and testing the Nelson-Phelps Technology Diffusion model (looks very solid), but there’s not enough space in a blog to discuss it. We also use a published estimate of the decline in genotypic intelligence to crudely predict the effect of dysgenics on the economy. The GDP per capita of western countries could be around 80% higher in 2100 if we could stop dysgenics now. 

So IQ has an extremely robust relationship with GDP. But in which way does the causality go - many of the IQ measurements used were taken during the growth period. Perhaps we have instead discovered that GDP very powerfully improves intelligence? That would be an interesting discovery too.

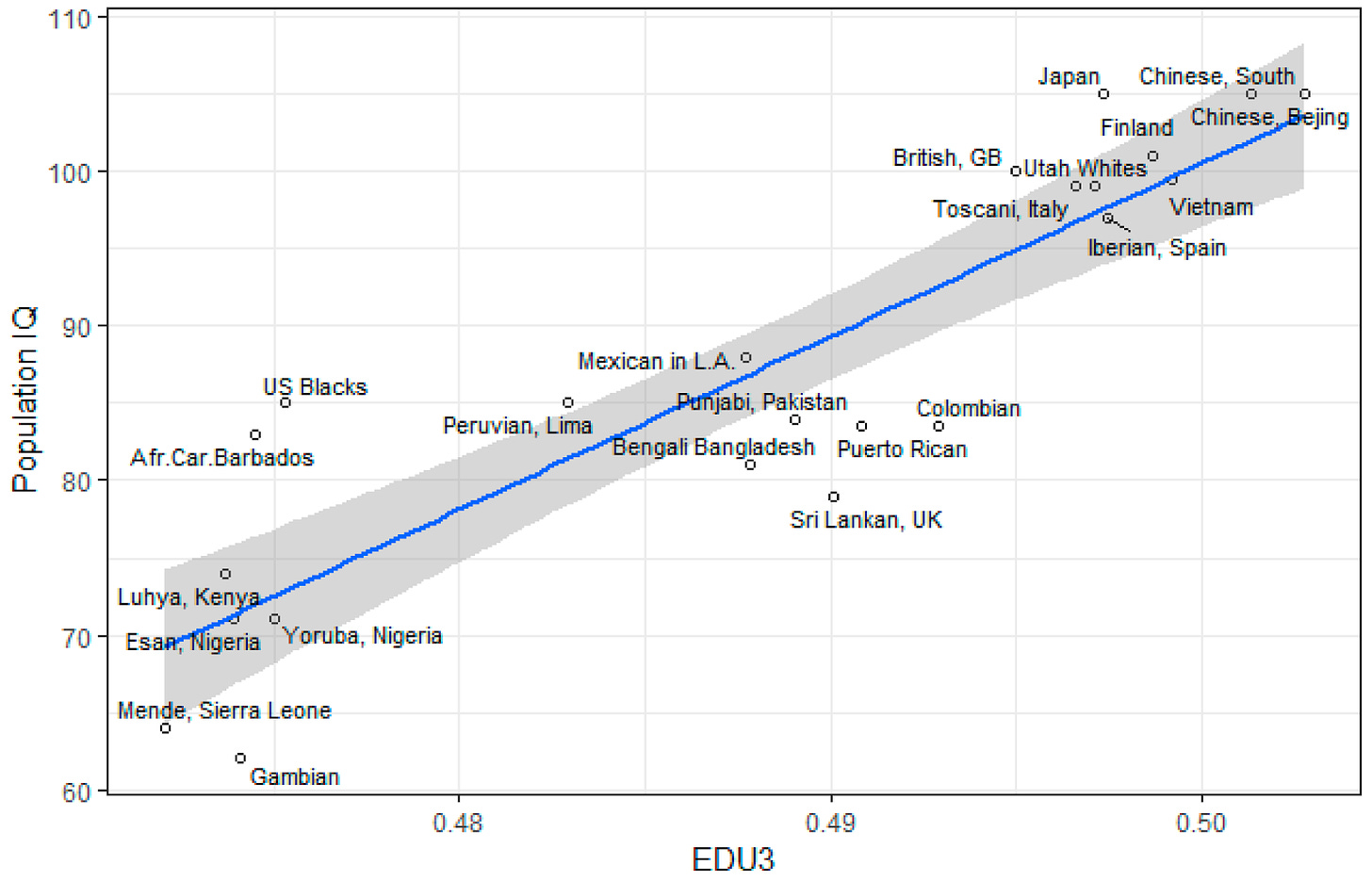
Nonetheless, we think our estimates very accurately measure a causal effect of IQ on GDP. For one, national IQs can almost be perfectly predicted (r = .9) from polygenic scores (EDU3) designed to estimate educational attainment. The as-of-yet unpublished results are even stronger with larger sample sizes. Although genetic prediction is currently far from perfect, the results are also far too strong to be coincidental. Even though environmental improvements could increase national IQ scores, the environment is itself a product of genes. Overall, it looks like national IQ nicely captures approximately static genetic differences in intelligence. 

More broadly, much of the past literature looking at this question provides good reason to think most of the causation goes from IQ to GDP. Diamond and oil-rich countries are no smarter than their neighbours. Using a reduced sample, national IQs measured before the growth period studied have the same effect size as when national IQs are measured during the growth period.

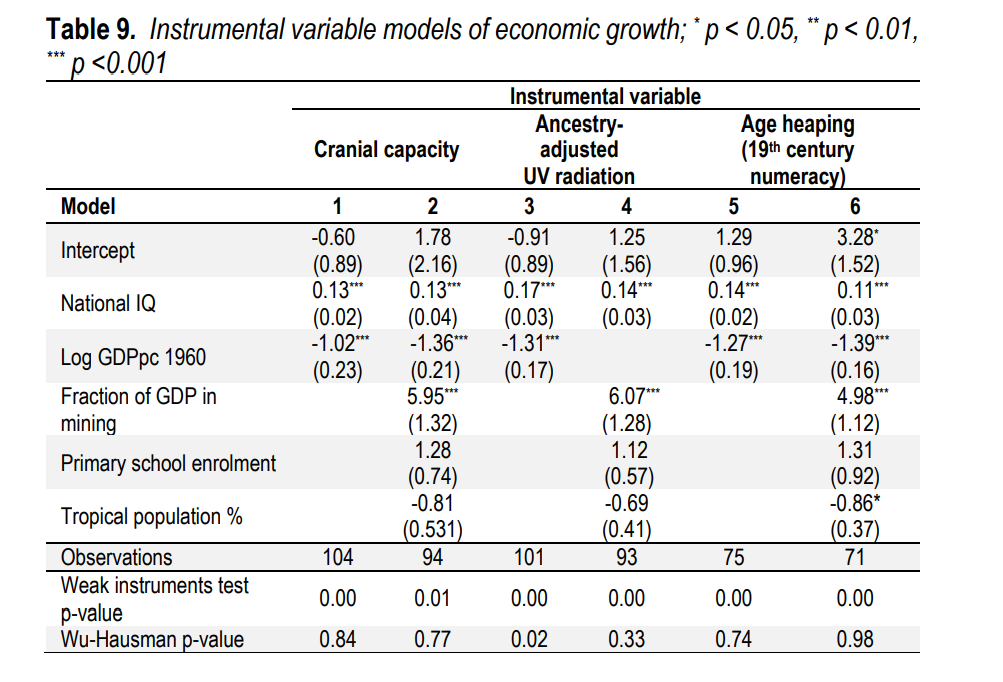
We contribute to the literature using a classic, bread and butter tool of econometrics - Instrumental Variable (IV) estimation. We wanted to identify a causal effect of national intelligence on growth, where growth cannot influence our measure of national intelligence. The trick is to use another variable that we believe causes national IQ but is not associated with economic growth through any other channel. Our instruments were cranial capacity (yes, average brain size in a country), ancestry-adjusted UV radiation, and 19th-century numeracy scores. For example, it is obvious that economic growth in the 20th century cannot influence numeracy in the 19th century. And by controlling for GDP per capita in the starting year, there should be no association between growth and 19th-century IQs, except through their effect on intelligence today. The IV estimates work by taking the effect of the instrument on economic growth and adjusting it for the instrument’s association with national IQ.

As expected our instrumented national IQ significantly predicts economic growth, suggesting that there is a causal effect. What is crucial in our table is the Wu-Hausman p-value. This tells us whether the coefficients in our IV estimates were significantly different from our regular regression estimates of the effect of national IQ (0.14 without controls, 0.11 with controls - which are also near identical to the estimates found with bayesian model averaging). If reverse causation substantially biases our estimates, then the IV estimate should be different from our normal estimates.

In only one of our six models was the Wu-Hausman test significant (p < 0.05), a result that could easily be obtained by chance. In that model, UV Radiation was our instrument and I suspect it probably correlates with geographical features that negatively effect growth, causing it to provide a different result. Supporting that conclusion,  when we controlled for a geographical variable, the percentage of the population living in tropical areas, the Wu-Hausman test was not significant. The possible effects of reverse causation only negligibly biased estimates of national IQ’s effect on economic growth.

To summarise, of all plausible explanatory variables, with the exception of past values of GDP, IQ best explains national variation in economic growth and conventional econometrics suggests the effect is causal. If you want to read more about intelligence and the economy then make sure to subscribe.